|
1. |
Change the linear equation
to "y=" form. |
y = -x + 4 |
|
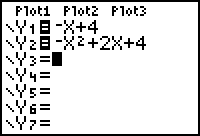
2. |
Enter
the equations as "y1=" and
"y2=".
(Be
sure to use the negative key, not the subtraction key, for
entering negative values.) |
|
|
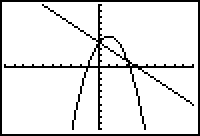
3. |
Hit GRAPH
to see if and where the graphs intersect.
(Using ZOOM
#6: ZStandard creates a 10 x 10
viewing window.
You may need to adjust the WINDOW to see a clear picture of the intersection locations for the
two graphs.) |
|
|
4. |
Under CALC (2nd
Trace) choose #5 intersect to find the points where the graphs intersect. |

|
|
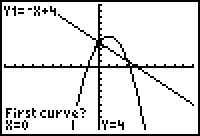
5. |
When prompted for the "First curve?", move the spider on,
or near, a point of intersection. Hit Enter. |
|
|
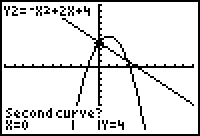
6. |
When prompted for the "Second curve?", just hit Enter.
|
|
|
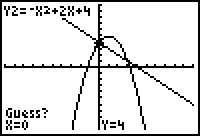
7. |
Ignore the prompt for "Guess?", and hit Enter.
|
|
|
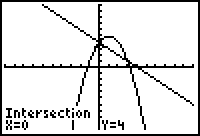
8. |
Read the answers as to the
coordinates of the point of intersection. These
coordinates appear at the bottom of the screen. Point of intersection
(left side): (0,4) |
|
|
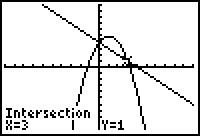
9. |
If your graphs have a
second point of intersection, repeat this process to find the
second point. Choose the #5
intersect choice and repeat the steps for finding the
intersection. Point of intersection (right side): (3,1) |
|


![]()