Graphing Circle Equations |
Graphing circle equations on the TI-Nspire can be accomplished in two options.
Graphing a circle is based upon the center-radius format:
(x - h)2 + (y - k)2 = r2
(h,k) = center of circle, r = radius of circle
|
 |
Graph Using the Graph Application: (Option 1: Center form) |
| |
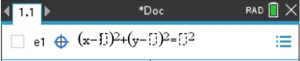
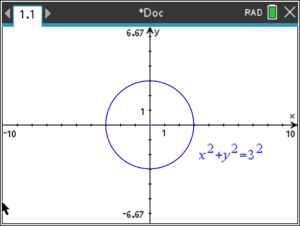
Graph x2 + y2 = 9
You need to know, or be able to find, the center and radius of the circle before you begin.
For this example, the center of the circle is (0,0), and the radius is 3. That is
(h,k) = (0,0), r = 3.
Option 1: Center form
• Start with a Document with #2 Add Graph.
•  , #3 Graph Entry/Edit, #3 Equation Templates, #3 Circle, #1 Center form
(x - h)2 + (y - k)2 = r2
• The "entry template" will appear as shown at the right.
•The entry becomes:
(x - 0)2 + (y - 0)2 = 32 |
"entry template"
|
Graphing a circle is based upon the standard format:
ax2 + ay2 + bx + cy + d = 0
|
Graph Using the Graph Application: (Option 2: Standard form) |
| |
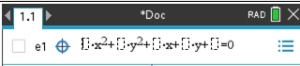
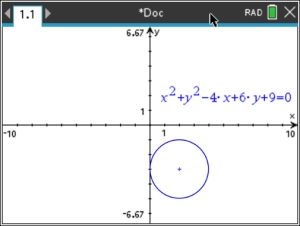
Graph x2 + y2 - 4x + 6y + 9 = 0
Option 2: Standard form
• Start with a Document with #2 Add Graph.
• , #3 Graph Entry/Edit, #3 Equation Templates, #3 Circle, #2 Standard form
ax2 + ay2 + bx + cy + d = 0
• The "entry template" will appear as shown at the right.
Note: If you want to use this equation, with Option 1, you will need to "complete the square" to find the center and radius.
(Such work was encountered in Geometry.) |
"entry template"
|
So, where did this "Standard form" come from?
Start with the "Center form" and expand:
(x - h)2 + (y - k)2 = r2
(x2 - 2xh + h2) + (y2 - 2yk + k2) = r2
x2 + y2- 2xh - 2yk + h2 + k2 = r2
x2 + y2 + (-2h)x + (-2k)y + h2 + k2 = r2
Remember: only the x and y are "variables" in this equation.
The other letters are "constants" (numbers).
Let's rename and combine the "constants":
Let b = -2h
Let c = -2k
Let d = h2 + k2 - r2
x2 + y2 + (-2h)x + (-2k)y + h2 + k2 - r2 = 0
x2 + y2 + bx + cy + d = 0
We know that in the equation for a circle, the coefficients of x2 and y2 must be the same.
So, to create a more "general" formula, that will include situations where the coefficients
of x2 and y2 are not 1 (and of course, not zero), we indicate the possibility of a coefficient of "a".
ax2 + ay2 + bx + cy + d = 0
These values of b, c and d are not equivalent to those from the previous equation (unless a = 1).
These values can be redefined to match this new situation.
Table of Contents | MathBits.com | Terms of Use
|
